【勉クラ】美しい比率を利用しよう【小6】

今回の勉クラは「比率」のお話です。

芸術の世界は感性がすべて……というわけでは決してなく、多くの人がより美しいと感じる定番の法則がいくつか存在します。

そのうちのひとつが「比率」です。

ざっくり言うと黄金比のようなものですが、他にもいろいろな種類があるのでまとめてご紹介したいと思います。

（正確な計算方法は割愛し、近似値でご紹介します。）

黄金比 (1:1.618)

誰でも一度は聞いたことあると思います。

芸術分野では最も美しい比率と言われています。

ある線分を2分割しそれぞれの線分の長さをa, bとしたとき、「a:b」が「b:(a+b)」に等しくなる比率のことを黄金比と言います。

白銀比 (1:1.414)

白銀比には2種類ありますが、ここでは普段よく目にする「1:1.414」を取り上げます。

この比率は「大和比」とも呼ばれ、日本の建築物などによく見られる比率とのこと。

和風建築にはぜひ取り入れていきたいですね。

また縦と横の長さが「1:1.414」となる長方形はルート長方形と呼ばれ、半分にしても縦横の比率が変わらないことから紙（A判、B判）の寸法としても使われています。

青銅比 (1:1.303)

黄金比、白銀比と同じ貴金属比のひとつです。

使用例はあまりないものの、美しい比率の1つと言われています。

白金比 (1:1.732)

こちらも芸術の世界では美しい比率の1つとされています。

貴金属の名前がついていますが、貴金属比ではないそうです。

青銅比同様、あまり使われた例はないようです。

ここからは、実際の数字ではなく美しい比率を考えるための「法則」についてご紹介します(*´ω｀*)

整数比

「1:2」や「1:3」など整数のみで表される比率です。

デザイン・芸術の世界でも明快さからよく利用されるようですが、マイクラは世界そのものがすでに整数比でできていると言えますね。

等差数列

3つ以上の数を考えるとき、それぞれの項の差が等しくなる数列です。

例「1:3:5:7:9...」（各項の差は2）

画像は3ブロックからから2ずつ増加した例。

等比数列

3つ以上の数を考えるとき、それぞれの項が等しい倍率となる数列です。

例「1:3:9:27...」（各項の倍率は3）

画像は2ブロックから1.5倍ずつ増加した例。（小数点以下四捨五入）

相加数列（フィボナッチ数列）

3つ以上の数を考えるとき、次の項が前の項2つの合計となる数列です。

フィボナッチ数列としても知られています。

「1:1:2:3:5:8:13...」となり、隣り合った2つの項は黄金比の近似値になるという性質があります。

おまけ：

アスペクト比（3:2、4:3, 16:9)

パソコンのモニターや映画のスクリーンなどに使われている縦横比のうち、特によく使われる3つの比率を上げてみました。

• 3:2 - カメラでよく使われる比率です。
• 4:3 - カメラや昔のモニターの解像度でよく使われています。
• 16:9 - ワイドモニターの解像度や映画のスクリーンでよく使われます。

ドット絵のスクリーンとしても活用できそうですね。

比率とブロックの計算方法

実際のブロックの計算方法はとても簡単です。

比率から係数を求め、実際のブロック数とかけ算をするだけです。

まず、基準となる線分の長さを30ブロックとして計算していきましょう。

（*「放物線」や「斜めの線」では1ブロック目を0として数えましたが、今回は長さなので1として数えます。）

具体的な計算方法は以下の通りです。

------------------------------------------------------------

まずは係数を求めます。

右の項を求める場合は「右÷左」、左の項を求める場合は「左÷右」を計算します。

最初に作った30ブロックを「4:3」の「4」としたい場合、求めたいのは「3（右の項）」のブロック数なので「3÷4」（右÷左）が係数となります。

3÷4 = 0.75

実際のブロック数に係数を掛け算します。

30 × 0.75 = 22.5

四捨五入します。

22.5 ≒ 23

------------------------------------------------------------

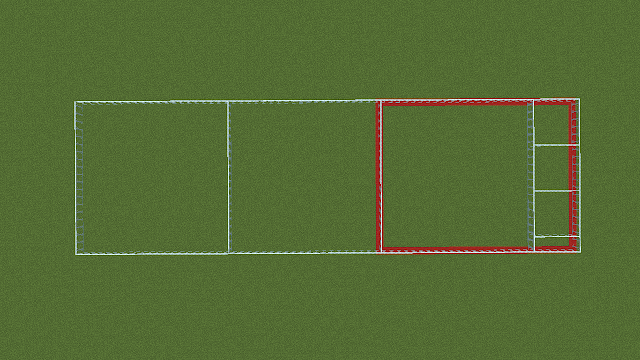
横30ブロック、縦23ブロックにすれば、およそ「4:3」の比率になるということがこれでわかりました。

実際にブロックを並べたのがこちらの画像です。

サイズが決まったら、あとは建てるだけ！

Let's build🐸

(初公開日：2020-04-18)